Why Modeling with Residual Checks Matters (and Why You Should Care)
If you’re preparing for AP Statistics or AP Precalculus, you’ve met regression models: linear fits, exponential curves, and maybe even a few more exotic beasts. But a model is only as useful as its ability to describe the world without lying to you. That’s where residuals come in — tiny numbers that reveal whether your model is a friend or a fraud.
Think of modeling as storytelling. Your scatterplot is the scene, the regression equation is the main character, and residuals are the narrator whispering, “Wait — that part doesn’t add up.” Learn to listen to those whispers and you’ll be doing more than solving an equation; you’ll be doing trustworthy analysis that exam graders and real-world scientists respect.

Quick Refresher: What Is a Residual?
A residual is the vertical distance between an observed data point and the value predicted by your regression model. If y_i is an observed value and ŷ_i is the predicted value from your model, the residual is:
residual = y_i − ŷ_i
Positive residuals mean the model underpredicted (the actual point sits above the line). Negative residuals mean it overpredicted (the point sits below the line). Residuals are the diagnostic tool that tells you where your model succeeds and where it stumbles.
Step-by-Step Workflow for Modeling with Residual Checks
This is a practical routine you can use on practice sets, homework, or during the AP exam. Treat it like a checklist.
- 1. Plot the data. Always start with a scatterplot. Look for clusters, outliers, gaps, or curves.
- 2. Consider candidate models. Is a linear model plausible? Exponential? Quadratic? Use context and visual shape to decide.
- 3. Fit the model. Use a graphing calculator, Desmos, or statistical software to compute the regression equation and R-squared.
- 4. Compute residuals and draw a residual plot. Plot residuals on the vertical axis against the explanatory variable (or predicted values) on the horizontal axis.
- 5. Interpret the residual plot. Look for randomness, patterns, non-constant spread (heteroscedasticity), and outliers.
- 6. Revise the model if necessary. If the residuals show structure, choose a different model or transform variables, then repeat checks.
- 7. Report results with context. State the model, summarize residual behavior, and explain practical implications or limitations.
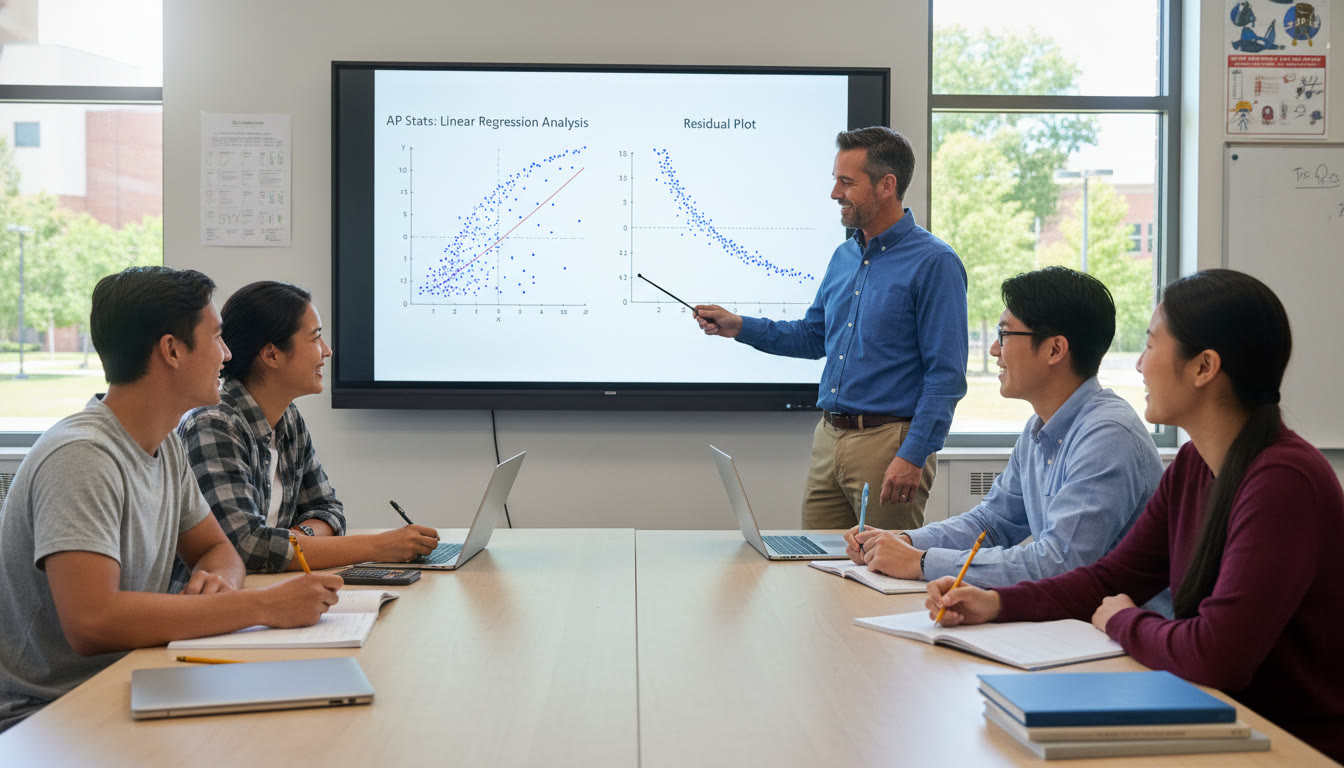
What to Look For in a Residual Plot (and What It Means)
Random Cloud — Good News
If residuals look like a random scatter centered around zero, the model captures the main pattern. Small, random residuals suggest your model is appropriate for prediction in the examined range.
Curved Pattern — Think Nonlinear
If residuals show a systematic curve (smile or frown), your linear model is missing curvature. Try a transformation (log, square root) or fit a nonlinear model (quadratic, exponential).
Funnel Shape — Watch for Heteroscedasticity
If residual spread increases or decreases with x (a funnel), variance isn’t constant. Predictions may be less reliable for certain x-values — consider weighted regressions or suitable transformations.
Outliers and High-Leverage Points
Large residuals call for investigation. Is the data point an error? An unusual but valid observation? High-leverage points (extreme x-values) can pull the regression line and distort inference. Don’t ignore them — explain them.
Worked Example: Interpreting Residuals Step-by-Step
Let’s walk through a compact, AP-style example. Suppose a researcher collects data on hours studied (x) and scores on a practice AP exam (y) for 20 students. A linear regression gives ŷ = 50 + 2.5x with R² = 0.68.
Compute residuals for each student (score − ŷ). When you plot residuals vs. hours studied, you notice the following:
- Most residuals cluster around zero from 0–6 hours.
- For 7–10 hours, residuals are mostly negative.
- One student at 0 hours had a very high positive residual (outlier).
Interpretation:
- Negative residuals at high study hours suggest the model overpredicts for students who study a lot — maybe marginal returns diminish, implying a logarithmic or concave model might fit better.
- The outlier at 0 hours needs context — maybe that student had prior knowledge or the practice score was anomalous.
- R² = 0.68 indicates a decent linear association, but residuals show systematic departure for high x — revise or report the limitation.
Example Table: Summary of Diagnostics
| Diagnostic | What You See | What It Suggests | AP Action |
|---|---|---|---|
| Scatterplot | Points lie roughly on a line | Linear model plausible | Fit linear regression and check residual plot |
| Residual Plot | Random cloud around zero | Model appropriate | Report model and use for prediction |
| Residual Plot | Systematic curvature | Nonlinear relationship present | Try transformations or nonlinear model |
| Residual Spread | Funnel shape | Non-constant variance | Consider transformation; be cautious with inference |
| Outliers | Large residuals or extreme x | Possible data issue or influential point | Examine in context; justify keeping or removing |
Choosing and Reporting Models on AP Exams
When an AP free-response question asks you to choose a model, graders look for reasoning based on the data and residual checks. Don’t simply quote R² — show you examined residuals and justified the choice.
- State the model explicitly and give the equation with appropriate rounding.
- Describe the residual plot: Is it random? Patterned? Any outliers?
- Conclude whether the model is “appropriate for prediction in the range of the data” or whether it “does not fit because residuals indicate curvature/heteroscedasticity.”
- When relevant, propose a specific adjustment (e.g., “Try a logarithmic transformation of x because residuals curve downward for large x”).
Common Mistakes and How to Avoid Them
Mistake: Relying Only on R²
R² tells how much variability is explained but not whether the model is appropriate. Always check residuals — high R² with a banana-shaped residual pattern still means the model is wrong.
Mistake: Ignoring Context
Numbers need context. A statistically significant slope might be practically meaningless; or an outlier might represent a valid subgroup. In AP answers, tie your statistical conclusion to the scenario.
Mistake: Blindly Removing Outliers
Don’t remove outliers without justification. If a point is a recording error, correct or drop it and explain why. If it’s a valid extreme, discuss its influence and consider robust methods or separate analysis.
Practical Tips for Exam Day
- Sketch quick residual plots when you do regression questions — even a rough cloud vs. x helps you notice major issues.
- Use consistent notation (y for response, x for explanatory, ŷ for predicted values, e for residuals) — clear notation helps graders follow your logic.
- When pressed for time, prioritize describing residual pattern and its implication over over-precision in coefficients.
- Practice with your graphing calculator so you can quickly compute and display residuals; AP Precalculus and AP Stats allow calculator-based regression and residual plotting.
When to Transform: A Simple Decision Guide
Transformations can straighten curvature or stabilize variance. Here are quick heuristic clues:
- If residuals curve up then down: try polynomial (quadratic) models.
- If residuals systematically decrease in spread after a log transform: try log(y) or log(x).
- If data grows proportionally (percentage change looks constant): exponential models (log y vs x) are natural.
Always re-check residuals after any transformation.
Mini Case Study: From Raw Data to a Robust Model
Imagine data tracking viral video views (y) vs days since release (x). Raw scatter suggests rapid early growth then leveling off. A linear fit gives decent R² but residuals show large negative values at high x (model overpredicts later performance).
Action plan:
- Fit a log transformation: model log(y) vs x. Residual plot now appears randomly scattered with smaller magnitude residuals.
- Interpret coefficients in context: the slope corresponds to multiplicative daily growth rates. Back-transform predictions carefully and state prediction intervals qualitatively (AP exam expects clear wording about interpretation and limits of extrapolation).
Study Strategy: How to Practice Residual Checks Efficiently
You’ll get the most improvement with targeted, active practice rather than hours of passive reading.
- Work on 12–15 representative datasets: linear, quadratic, exponential, heteroscedastic, and with outliers.
- For each dataset, follow the step-by-step workflow above and write a one-paragraph interpretation like you would on the exam.
- Time yourself: practice doing the whole pipeline in 10–15 minutes to build exam stamina.
- Check your reasoning with an instructor or peer — explaining why you chose a model increases retention.
If you want guided practice, consider a few sessions of targeted tutoring: Sparkl’s personalized tutoring offers 1-on-1 guidance, tailored study plans, and expert tutors who can walk through residual checks with you and provide AI-driven insights to speed learning. A short series of coached problem sets can dramatically sharpen your ability to spot modeling pitfalls under exam conditions.
Common AP Free-Response Phrases That Score Well
- “The residual plot shows…” followed by a concise description (random/curved/funnel/outlier).
- “Therefore, a linear model is/ is not appropriate for prediction in the range of the data because…”
- “I recommend trying…” (state a transformation or model type and why, based on residual behavior).
- “Extrapolation beyond the observed x-range is not recommended because…” (always mention extrapolation limits when asked to predict outside the data range).
How Graders Think — And How That Helps You Write Better Answers
AP readers look for evidence of statistical thinking. Residual analysis shows higher-level understanding because it moves beyond mechanical computation to model assessment. That’s why a paragraph describing residuals can be the difference between a partial and full-credit response.
Wrapping Up: A Short Checklist to Memorize
Keep this in your pocket as a mental checklist on test day:
- Plot data → Fit model → Plot residuals.
- Check for randomness, patterns, spread changes, and outliers.
- Explain whether the model is appropriate with context-based reasoning.
- Propose a specific fix when residuals misbehave and re-check.
- State limits of prediction and handle outliers transparently.
Final Thoughts — Modeling as an Iterative Conversation
Modeling with residual checks is less like a single exam question and more like a short conversation with your data. You fit a model, you listen to the residuals, you revise, and the model becomes a more honest companion. Over time, you’ll internalize the visual cues and language graders want.
Remember: the goal isn’t just to get the right numbers — it’s to communicate what the numbers mean. With regular practice, quick diagnostic checks, and occasional guided tutoring sessions (for instance, short bursts of 1-on-1 time to debug sticky residual patterns), you’ll be prepared not only for AP exam problems but also for real-world data decisions.
Quick Resources to Keep Handy
On your own, build a small folder with: practice datasets, one-page cheat-sheets for transformations, saved calculator instructions for residual plots, and a short rubric you write yourself for interpreting residual behavior. If you’re short on time, work with a mentor who can personalize those items to your strengths — Sparkl’s tailored study plans and AI-driven insights can help identify which residual patterns you misinterpret and accelerate your improvement.
Good Luck — and Trust the Residuals
When in doubt, plot the residuals. They are the honest second opinion your model can’t fake. Take them seriously, practice interpreting them often, and you’ll find modeling becomes one of your most reliable tools on exam day and beyond.



















No Comments
Leave a comment Cancel