Why Fluids and Thermo Matter (and Why You Can Own This Section)
If you’re prepping for AP Physics 2, you’ve probably noticed that fluids and thermodynamics show up in both conceptual and math-heavy questions. These topics feel everywhere: from why airplanes fly to how your soda can fizz when shaken. The good news? Fluids and thermodynamics follow clear rules — once you learn how to translate words into equations and intuition, they become powerful tools, not scary monsters.

What this article gives you
- Clear explanations of density, pressure, Bernoulli’s principle, and PV = nRT.
- Worked examples that mirror AP-style reasoning (concept + math).
- Study and exam strategies — including how to practice efficiently and how tailored tutoring can speed your progress.
- A compact table you can print and tuck into a formula sheet.
Part I — Density and Pressure: The Foundations
Density: What it actually means
Density is simply mass per unit volume. Symbolically, density ρ (rho) = m / V. That’s it. But the consequences are everywhere. Density tells you whether an object floats, how waves travel through media, and why hot air rises.
Practical tips:
- Keep units consistent: kilograms and cubic meters (kg/m³) for SI; grams and cubic centimeters (g/cm³) are common in lab settings. 1 g/cm³ = 1000 kg/m³.
- Relative density (specific gravity) is density compared to water. If something has specific gravity less than 1, it floats in water.
Pressure: force spread out
Pressure is force per unit area: P = F / A. In fluids, pressure at a point depends on depth (for static fluids), but not on the shape of the container. That last fact is a gateway to many AP-style questions.
- Units: Pascals (Pa) = N/m² are preferred. You’ll see atmospheres (atm), torr, and mmHg in thermo problems — convert when needed (1 atm ≈ 1.01 × 10^5 Pa).
- Hydrostatic pressure: P = P0 + ρ g h, where P0 is pressure at the surface (often atmospheric), ρ is fluid density, g is gravitational acceleration, and h is depth below the surface.
AP-style Example: Will it float?
Imagine a block of wood of mass 2.5 kg and volume 0.003 m³ placed in water (ρwater ≈ 1000 kg/m³). Density of wood ρ = 2.5 / 0.003 ≈ 833.3 kg/m³, which is less than water, so it floats. The displaced water mass equals the block mass when floating: displaced volume = m / ρwater = 2.5 / 1000 = 0.0025 m³, so 0.0025 / 0.003 ≈ 83% of the block’s volume is submerged.
Part II — Bernoulli’s Principle: Flowing Fluid Intuition
What Bernoulli actually says
Bernoulli’s equation (for steady, incompressible, non-viscous flow) is an energy statement along a streamline: P + 1/2 ρ v² + ρ g y = constant. It relates pressure (P), kinetic energy per volume (1/2 ρ v²), and potential energy per volume (ρ g y).
In words: when a fluid speeds up, pressure tends to drop (if height stays the same). When a fluid rises in height, pressure decreases because energy is converted into gravitational potential.
Common AP scenarios
- Constricted pipes: flow speeds up through a narrow section, so static pressure drops there.
- Venturi effect and flow meters: use pressure differences to measure speed.
- Lift on a wing: simplified explanations use Bernoulli to show pressure differences above and below the wing, contributing to lift (there are also other factors like circulation and Newton’s third law, but Bernoulli is a great start for AP-level reasoning).
How to approach Bernoulli problems
- Identify two points on the same streamline.
- Write Bernoulli’s equation for both points and set them equal.
- If volume flow rate is conserved (incompressible flow), use A1 v1 = A2 v2 to relate velocities.
- Be careful with gauge vs. absolute pressure — many AP problems want pressure differences, so atmospheric cancels out.
AP-style Example: Flow Speed from Pressure Drop
Water flows horizontally from a wide pipe (A1) into a narrower pipe (A2). Pressure in the wide section is P1 and in narrow section P2. Using Bernoulli (with y terms canceling for horizontal): P1 + 1/2 ρ v1² = P2 + 1/2 ρ v2². If v1 is small and P1 > P2, solve for v2: v2 = sqrt((2/ρ)(P1 – P2)). This neat relation is often useful for problems where upstream speed is negligible.
Part III — Thermodynamics: The Ideal Gas Law and Beyond
PV = nRT — the essential form
The ideal gas law packs macroscopic behavior into PV = nRT. P is pressure, V is volume, n is number of moles, R is the ideal gas constant (R ≈ 8.314 J/(mol·K)), and T is temperature in Kelvin. Use this to link pressure, volume, and temperature in gas problems.
Quick reminders:
- Temperature must be in Kelvin. To convert from Celsius: T(K) = T(°C) + 273.15.
- If the problem uses particles instead of moles, use PV = NkT, where k is Boltzmann’s constant (k ≈ 1.38 × 10^-23 J/K) and N is number of molecules.
Process types: isothermal, isobaric, isochoric, adiabatic
AP Physics 2 commonly tests how heat and work change under different thermodynamic processes. Here’s a quick cheat-sheet:
- Isothermal (T constant): PV = constant. Work done by gas: W = nRT ln(Vf/Vi).
- Isobaric (P constant): Pressure constant so W = PΔV.
- Isochoric (V constant): No work done (W = 0); heat changes internal energy only.
- Adiabatic (no heat exchange): PV^γ = constant (for ideal gas), where γ = Cp/Cv. Temperature and pressure change without heat flow in or out.
Example: Balloon in a Cold Room
Suppose a sealed balloon contains 0.10 mol of an ideal gas at 300 K and 1.00 atm occupying volume V. If the temperature drops to 270 K while the balloon remains flexible and pressure remains atmospheric, what’s the new volume? Use PV = nRT: V ∝ T for constant P. So Vf = Vi * (Tf/Ti) = Vi * (270/300) = 0.9 Vi. A 10% drop in T produces a 10% drop in volume for a constant-pressure scenario — simple proportionality is an AP favorite.
Concrete Table: Quick Reference for Fluids & Thermo
| Concept | Key Equation(s) | When to Use |
|---|---|---|
| Density | ρ = m / V | Mass-volume relations, buoyancy |
| Hydrostatic Pressure | P = P0 + ρ g h | Pressure at depth in static fluids |
| Bernoulli (steady flow) | P + 1/2 ρ v² + ρ g y = constant | Relate pressure and velocity along streamlines |
| Continuity | A1 v1 = A2 v2 | Conservation of volume flow rate (incompressible) |
| Ideal Gas Law | PV = nRT | Relate P, V, T for gases |
| Isothermal Work | W = nRT ln(Vf/Vi) | Work done in isothermal processes |
How to Tackle AP Questions: A Step-by-Step Strategy
1) Read the prompt carefully
AP questions often hide a simple physics idea behind a verbose setup. Circle what’s given and what’s asked. Is pressure absolute or gauge? Is flow assumed incompressible? Check for words like “steady” or “quasi-static.”
2) Draw a picture and choose control points
For Bernoulli problems, draw the streamline and label velocities, heights, and pressures. For PV = nRT, sketch initial and final states and identify the process (isothermal, isobaric, etc.).
3) Choose the right equation and simplify
Match the concept to an equation: hydrostatic pressure for depth, Bernoulli for flow, PV = nRT for gases. Cancel common terms (like atmospheric pressure) early if possible.
4) Watch units and significant figures
AP graders penalize unit errors. Convert to SI where necessary and carry units through your algebra to avoid mistakes. Round at the end.
5) Do a reality check
- Does a computed pressure make physical sense (not negative unless gauge)?
- If a computed speed is faster than the speed of sound and the problem assumed incompressible flow, that’s a red flag.
Common Conceptual Traps (and how to beat them)
1) Pressure is not the same as force
Pressure = force / area. A large pressure acting over a small area gives a small total force; the same pressure over a large area gives a large force.
2) Static fluid pressure acts in all directions
Water pushes sideways on a container wall just as it pushes downward. This is why dams are thicker at the bottom: pressure increases with depth.
3) Bernoulli’s limits
Bernoulli assumes steady, incompressible, non-viscous flow along a streamline. If there’s turbulence, viscosity, or compressible speeds (high Mach number), Bernoulli needs modification. On the AP exam, the question will usually make these assumptions explicit or imply them with wording like “ideal fluid” or “incompressible flow.”
Practice Problems (with quick solutions)
Problem 1 — Buoyancy check
A metal cube of side 0.05 m has mass 0.8 kg. Will it float in oil with density 920 kg/m³? Compute cube volume V = 0.05³ = 1.25 × 10^-4 m³. Density of cube ρ = 0.8 / 1.25e-4 ≈ 6400 kg/m³. Since 6400 > 920, it sinks. Quick, clean, and exactly the kind of reasoning an AP grader likes.
Problem 2 — Venturi pressure drop
Water flows from a section of pipe of area 0.04 m² at 0.5 m/s into a narrower section of area 0.01 m². Find the speed in the narrow section and the pressure difference (assume horizontal and ρ = 1000 kg/m³). Using continuity: v2 = (A1 v1) / A2 = (0.04 × 0.5)/0.01 = 2.0 m/s. Bernoulli (with points 1 and 2 horizontal): P1 + 1/2 ρ v1² = P2 + 1/2 ρ v2² ⇒ P1 – P2 = 1/2 ρ (v2² – v1²) = 0.5 × 1000 × (4 – 0.25) = 0.5 × 1000 × 3.75 = 1875 Pa. So the narrow section has 1875 Pa lower static pressure.
Problem 3 — Gas law quick change
A 2.00 L container holds 0.0820 mol of an ideal gas at 300 K. What is the pressure? Convert to SI: V = 0.00200 m³. Use PV = nRT ⇒ P = nRT / V = (0.0820 × 8.314 × 300)/0.00200 ≈ (204.5)/0.002 = 1.02 × 10^5 Pa ≈ 1.01 atm. Numbers align with everyday intuition — a good AP sanity check.
Study Plan: How to Make Progress Without Burning Out
Weekly structure for two months before the exam
- Week 1–2: Conceptual building. Spend short, focused sessions on density, pressure, hydrostatics. Do 10–15 conceptual multiple-choice questions per day.
- Week 3–4: Bernoulli and continuity. Mix conceptual questions with algebraic practice: relate velocities to pressures and areas.
- Week 5–6: Thermodynamics and gas laws. Practice PV = nRT problems and different process types with emphasis on work and heat signs.
- Week 7–8: Mixed practice and full-length timed sections. Review mistakes, practice free-response format, and simulate exam timing.
Active study techniques
- Explain solutions out loud like you’re teaching a friend — this reveals gaps in your reasoning.
- Create a one-page cheat sheet of equations and the conditions when they apply (Bernoulli only for steady, incompressible flow, etc.).
- Do “error journals”: for every practice question you miss, write 1–2 sentences explaining the mistake and what to do differently next time.
How Personalized Help Speeds Your Progress
Self-study is powerful, but targeted guidance accelerates progress. Personalized tutoring can help identify your weakest conceptual threads, tailor practice problems to your gap areas, and model exam-style reasoning. For example, Sparkl’s personalized tutoring offers 1-on-1 guidance, tailored study plans, expert tutors, and AI-driven insights that can highlight the one or two assumptions you repeatedly miss — saving hours of blind practice. When the tutor works through free-response questions with you, they’re not just giving answers; they’re showing the compact, score-earning reasoning AP graders want to see.
Exam Day Strategies and Common Pitfalls
Timing and question order
Start multiple-choice with questions you find easiest to build confidence. For free response, attempt the ones worth more points early so you have time to refine your answers. If a derivation is messy, write the key equations and explain each step — partial credit is significant.
Writing free-response answers
- Label diagrams clearly. A small sketch with directions, forces, or streamlines often secures method points.
- State assumptions: “assume incompressible, steady flow” — that shows your awareness and prevents misinterpretation.
- Box final numerical answers, include units, and show intermediate algebraic steps when you can.
Common small errors to avoid
- Forgetting to convert temperature to Kelvin.
- Mixing up gauge and absolute pressure without adjusting appropriately.
- Dropping density units or using inconsistent units for g (m/s² vs ft/s²).
Wrap-Up: Building Confidence and Intuition
Fluids and thermodynamics reward careful reading, consistent units, and clear diagrams. Start from simple principles — conservation of mass (continuity), conservation of energy (Bernoulli), and the ideal gas law — and practice translating words into equations. Over time, the messy, multi-step problems become more like puzzles with predictable moves.
If you want to maximize your score efficiently, consider mixing focused practice with tailored guidance. A few targeted sessions that fix a recurring misconception can be worth many hours of solo study. Tools like Sparkl’s personalized tutoring can provide that targeted coaching: 1-on-1 sessions that identify your blind spots, tailored study plans to close them, and AI-driven insights to track your progress.
Final encouragement
Physics 2 is a test of clarity more than brute force. Keep your formulas in a neat mental toolbox, sketch deliberately, and check answers with dimensional reasoning and common-sense limits. With steady, purposeful practice you’ll convert daunting problems into manageable, point-rich steps. Go into the exam curious, calm, and confident — you’ve got this.
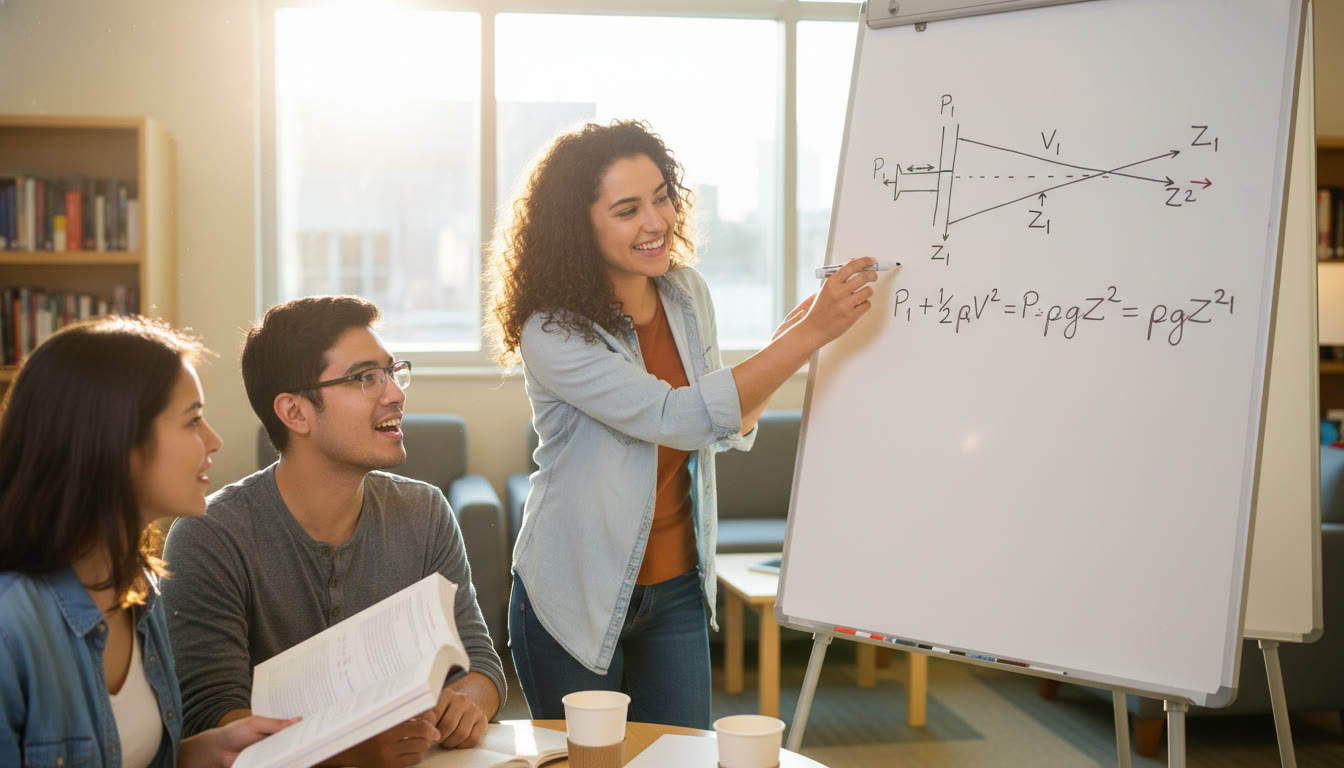
























No Comments
Leave a comment Cancel