Geometry in the SAT: What Still Shows Up
If you blinked when the SAT redesigned its math sections, you are not alone. Geometry used to feel like a separate beast in older tests; today it’s woven into algebra, problem solving, and the occasional standalone geometry question. That can make preparation feel fuzzy: what should you actually study? What patterns repeat? And how do you translate geometric intuition into fast, correct answers on test day?
Why geometry still matters
Here’s the short version: geometry still shows up often enough that ignoring it is a risky strategy. Whether the question is phrased as a pure shape problem, a coordinate-geometry task, or a word problem hiding a triangle, the test rewards students who can visualize, label, and apply a handful of reliable facts quickly. In other words, geometry is practical — not exotic. Spend time on the essentials and you’ll pick up points that other students miss.
How geometry appears on the modern SAT
Rather than a separate section labeled ‘Geometry’, the SAT integrates geometric reasoning across the Math Test. Expect to see geometry in three broad ways:
- Classic shape questions: Areas, perimeters, angles, circles, and polygons presented on diagrams.
- Coordinate geometry: Points, slopes, distances, midpoints, equations of lines, and areas placed on the coordinate plane.
- Geometry inside algebra: Similar triangles used to find lengths, right-triangle problems solved with the Pythagorean theorem, and geometry-based ratios in word problems.
That means proficiency in both pure geometric facts and algebraic manipulation pays off — a double win for focused study.
What’s most likely to show up?
Based on released practice tests and the structure of the exam, some geometry topics appear more commonly than others. The next table organizes common topics into a simple ‘High/Medium/Low’ frequency guide so you can prioritize study time.
| Topic | Typical SAT Focus | Why it matters |
|---|---|---|
| Triangles (Pythagorean, special triangles, similarity) | High | Used in standalone problems and hidden in word problems; essential for many coordinate problems. |
| Circles (radius, diameter, chord, arc relationships) | Medium | Questions may ask for area, circumference, or relationships involving inscribed angles. |
| Polygons (interior/exterior angles, area) | Medium | Understanding angle sums and regular polygons helps with angle-chasing and area problems. |
| Coordinate geometry (slope, distance, midpoint, line equations) | High | Easy to combine with algebra; many problems are more straightforward in coordinates. |
| 3D geometry (volume, surface area) | Medium | Often appears as a simple formula application or composite solid problem. |
| Transformations and trigonometry | Low | Basic ideas may appear, but intensive trig or advanced transformation proofs are rare. |
Essential geometry toolbox: formulas and quick facts
Memorize and understand these. They appear again and again — not because the test is flashy, but because the problems are efficient when you have the right facts ready.
- Pythagorean theorem: a^2 + b^2 = c^2 (right triangles)
- Special right triangles: 45-45-90 (legs x, hypotenuse x√2); 30-60-90 (short leg x, long leg x√3, hypotenuse 2x)
- Area formulas: triangle = 1/2 * base * height; rectangle = length * width; circle = πr^2; trapezoid = 1/2 * (b1 + b2) * height
- Circumference: 2πr (or πd)
- Polygon interior angle sum: (n – 2) * 180°; regular polygon interior angle: ((n – 2)*180°)/n
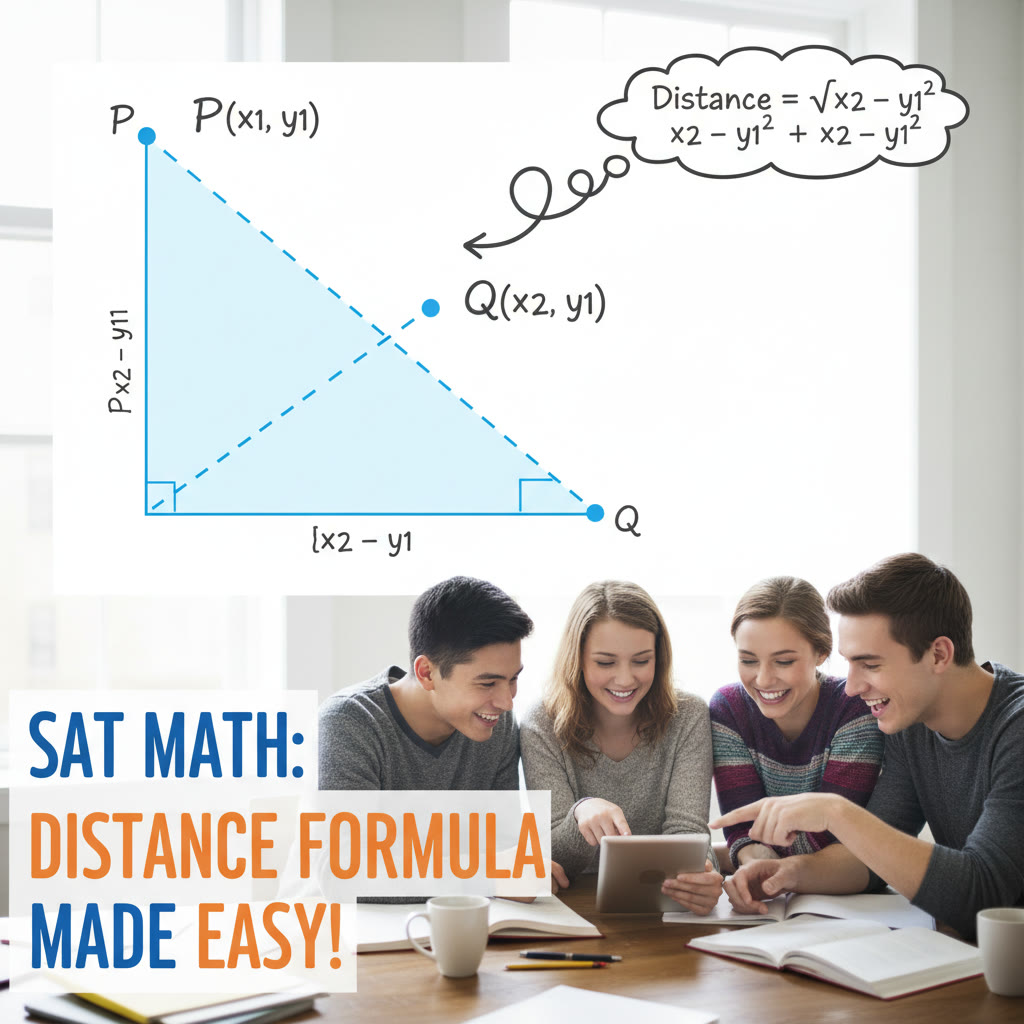
- Slope: (y2 – y1)/(x2 – x1); Distance: sqrt((x2 – x1)^2 + (y2 – y1)^2); Midpoint: ((x1 + x2)/2, (y1 + y2)/2)
- Similar triangles: corresponding sides are proportional; corresponding angles equal
Visual habits that win points
Geometry is as much about how you look at a problem as what you know. Train these habits:
- Redraw or straighten. If a diagram is slanted or labels are messy, redraw a cleaner version and mark right angles and equal lengths.
- Label everything. If the text says two segments are equal, write an equal mark. If a point is the midpoint, show that on your diagram.
- Decide whether coordinates help. If numbers or slopes would simplify the problem, place the figure on the coordinate plane.
- Work from what’s given to what’s asked. If you’re asked for a length, list which theorems or formulas connect the givens to that length.

Worked examples: learn by doing
Below are three sample problems that mirror the kinds of geometry questions you’ll see on the SAT. Read the setup, try each yourself, then check the solution steps.
Example 1 — Right triangle and altitude (classic Pythagorean)
Problem: In right triangle ABC, angle C is 90°. AC = 6 and BC = 8. What is the length of AB? (Round only if necessary.)
Solution: Recognize the triangle is right with legs 6 and 8. Use the Pythagorean theorem: AB^2 = AC^2 + BC^2 = 6^2 + 8^2 = 36 + 64 = 100. So AB = 10.
Why this is typical: Short, clean numbers force you to pick the Pythagorean theorem quickly. If you saw a number like 9 and 12 instead, you could factor out a common multiple or move to special triangles if appropriate.
Example 2 — Similar triangles hidden in a diagram
Problem: Triangle ABC and triangle ADE are similar. Points D and E lie on sides AB and AC respectively. If AB = 12, AD = 4, and AE = 3, what is AC?
Solution: Similar triangles mean corresponding sides have proportional lengths. AD corresponds to AB in the larger triangle if D is a point on AB and E on AC producing a smaller, similar triangle at the corner A. The scale factor from the small triangle ADE to the big triangle ABC is AB/AD = 12/4 = 3. The same scale factor applies to AE and AC, so AC = 3 * AE = 3 * 3 = 9.
Tip: Draw little tick marks to identify corresponding sides. Once you spot similarity, the rest is proportion arithmetic — and that’s fast.
Example 3 — Coordinate geometry and distance
Problem: Points P and Q have coordinates P(−2, 5) and Q(4, −1). What is the length of PQ?
Solution: Use the distance formula, which is the Pythagorean theorem in coordinates: PQ = sqrt((4 − (−2))^2 + (−1 − 5)^2) = sqrt((6)^2 + (−6)^2) = sqrt(36 + 36) = sqrt(72) = 6√2.
Why coordinate skills matter: Many problems that seem geometric are easiest when you move to coordinates. If you can shift betwen pure geometry and coordinate methods fluidly, you’ll save time.
Practice problem you can time yourself on (try it in 3–4 minutes)
Problem: A circle has center O and radius 6. Chord AB is a distance of 4 from the center O. What is the length of chord AB?
Suggested approach: Draw a radius to the midpoint of the chord and form a right triangle. Let M be midpoint of AB. OM = 4, OA = 6. Then AM = sqrt(6^2 – 4^2) = sqrt(36 – 16) = sqrt(20) = 2√5. So AB = 2 * AM = 4√5.
Note: This problem tests geometry + right-triangle thinking + the property that the perpendicular from the center to a chord bisects the chord.
Smart guessing and answer-checking strategies
Sometimes the SAT gives you answer choices that make a problem faster if you work backwards or plug in. Here are a few reliable moves for geometry:
- Plug in numbers: If a problem is about proportional relationships or similar triangles with variables, substitute practical numbers to test options.
- Backsolve: Try answer choices in a diagram or equation, especially when choices are numeric and limited.
- Estimate with bounds: If you only need an approximate comparison, use rough area or length bounds to eliminate extreme choices.
- Use symmetry: If a figure is regular or symmetric, exploit that to simplify calculations (for instance, equal angles and sides).
Time management: where geometry fits in your pacing
The SAT math sections reward quick, accurate problem solving. Geometry problems can be quick if you spot the right idea; they can also be time sinks if you start algebra without first labeling a diagram. Use this pacing plan:
- Scan the question: If a diagram is included, study it for 10–15 seconds to mark givens and look for right angles, parallel lines, or congruent marks.
- Do the easy ones fast: If it’s straightforward (like basic Pythagorean or slope), do it and move on.
- Mark doubtfully hard geometry questions and skip them initially. Return with fresh time and clearer perspective; sometimes coordinate substitution or plugging answers makes them trivial.
Study plan: how to prepare for SAT geometry in 6 weeks
Here’s a practical, compact plan you can adapt. The focus is depth over rote memorization — understand a few ideas well rather than many shallowly.
- Week 1: Master the basics — Pythagorean theorem, area formulas, circle basics, and special triangles.
- Week 2: Work on triangle similarity and congruence, practice ratio and proportion problems, and do 10 geometry practice problems every other day.
- Week 3: Coordinate geometry — slope, distance, midpoint, equation of a line. Translate a handful of classic geometry problems into coordinates.
- Week 4: Polygons and angle chasing — interior/exterior angles, parallel lines, and transversals. Practice with diagrams and learn to mark equal angles.
- Week 5: 3D geometry basics — surface area and volume of prisms, cylinders, cones, and spheres. Do composite solid problems.
- Week 6: Mixed practice and timed sections — combine geometry with algebra and practice under timed conditions. Review mistakes and drill weak facts.
If you have limited time or want a plan tailored to your starting point, consider targeted help. Sparkl’s personalized tutoring can offer 1-on-1 guidance, tailored study plans, expert tutors, and AI-driven insights to pinpoint gaps and speed up progress. Small course corrections from an expert can make a big difference in a few weeks.
Common pitfalls and how to avoid them
Geometry mistakes are rarely about computation alone — they often come from misreading figures or assuming unlabeled facts. Watch out for these traps:
- Assuming right angles where none are marked. Only marked right angles count.
- Confusing similar and congruent. Similar triangles have proportionate sides, congruent triangles have equal sides and angles.
- Forgetting that midpoints bisect segments — that gives you equal segments to use in ratios.
- Relying on drawn-to-scale diagrams. They’re a guide, not a guarantee. Always base reasoning on given information.
How practice should feel: quality over quantity
Doing hundreds of problems indiscriminately can burn you out. Instead, aim for deliberate practice:
- Practice a set of diverse problems, time yourself, and then review each mistake carefully.
- When you miss a geometry question, recreate the problem from memory and solve it again — this forces stronger encoding of the technique.
- Keep a ‘geometry mistakes’ notebook of the patterns that trip you up (angle-chasing errors, forgetting midpoint properties, algebra mistakes inside geometry). Revisit this weekly.
Final checklist before test day
Run down this quick checklist in the final week to make sure your geometry skills are exam-ready:
- I can calculate slope, distance, and midpoint quickly on scratch paper.
- I have the area and circumference formulas memorized for circles and polygons.
- I can recognize and use special right triangles without reaching for a calculator.
- I can translate a diagram into variables and equations when needed.
- I have practiced at least five full, timed sections that mix geometry with algebra.
Wrapping up: think of geometry as an efficiency tool
Geometry on the SAT rewards students who can combine visualization with algebraic discipline. Instead of a separate subject to fear, think of geometry as a toolbox of shortcuts: the right figure, a labeled diagram, and a single proportion can turn a confusing problem into a 30-second answer. With a compact set of facts and a few practiced habits, you’ll find more points with less time wasted.
If you want to accelerate progress, personalized coaching can help. Sparkl’s personalized tutoring blends expert tutors and AI-driven insights to create tailored study plans and 1-on-1 guidance — the kind of focused help that turns weak spots into reliable strengths.
Study deliberately, practice with purpose, and remember: geometry on the SAT is less about memorization and more about seeing what the problem is asking. Turn that angle into an advantage, and you’ll carry points from geometry straight into your final score.

















No Comments
Leave a comment Cancel