AP Precalculus Unit 1 Deep Dive: Functions & Modeling
Why Unit 1 Matters — and Why You Should Care
Unit 1 of AP Precalculus sets the stage for the whole course. Functions and modeling are more than just formulas on a page — they are the language we use to describe change, pattern, and relationship in science, engineering, economics, and everyday life. If you master this unit, the rest of the course becomes less about memorization and more about powerful ways of thinking.
What You’ll Learn in This Unit (At a Glance)
Unit 1 typically covers foundational concepts that reappear across the AP Precalculus exam and in real-world applications. Expect to build confidence in:
- Definitions and representations of functions (tabular, graphical, algebraic, and verbal).
- Function behavior: domain, range, injective/surjective properties, and inverses.
- Types of functions you’ll meet often: linear, polynomial, rational, exponential, logarithmic, trigonometric, and piecewise.
- Modeling real-world data with appropriate function families and evaluating fit.
- Transformations: shifts, stretches/compressions, reflections, and compositions.
- Connecting algebraic manipulations with graphical intuition.
Core Concepts — Clear, Practical Explanations
1. What Is a Function?
A function links each input (usually x) to exactly one output (usually f(x)). Think of it as a machine: you feed in a number, the machine follows rules, and it returns a single number. Representations matter: the same function can appear as a table of values, a graph, an equation, or a description in words. Being fluent in moving between these forms is essential.
2. Domain and Range — What Values Are Allowed and Produced
Domain = all allowable inputs. Range = all possible outputs the function actually produces. When modeling, choosing the correct domain is as important as the equation itself — real-world problems often restrict domains (time can’t be negative; population counts are nonnegative integers, etc.).
3. Function Types and When to Use Them
Knowing common function shapes helps you choose the best model for a problem. Here’s a quick road map:
- Linear: constant rate of change — good for simple proportional relationships.
- Polynomial: smooth curves that can change direction — useful for trajectories, approximations.
- Rational: ratios of polynomials — handy when behavior includes asymptotes or rates that change dramatically.
- Exponential: multiplicative growth or decay — essential for populations, radioactive decay, and interest problems.
- Logarithmic: inverses of exponential; useful when something grows quickly and then slows.
- Trigonometric: periodic behavior — waves, cycles, and anything repeating.
- Piecewise: different rules for different intervals — great for systems with stage-based behavior.
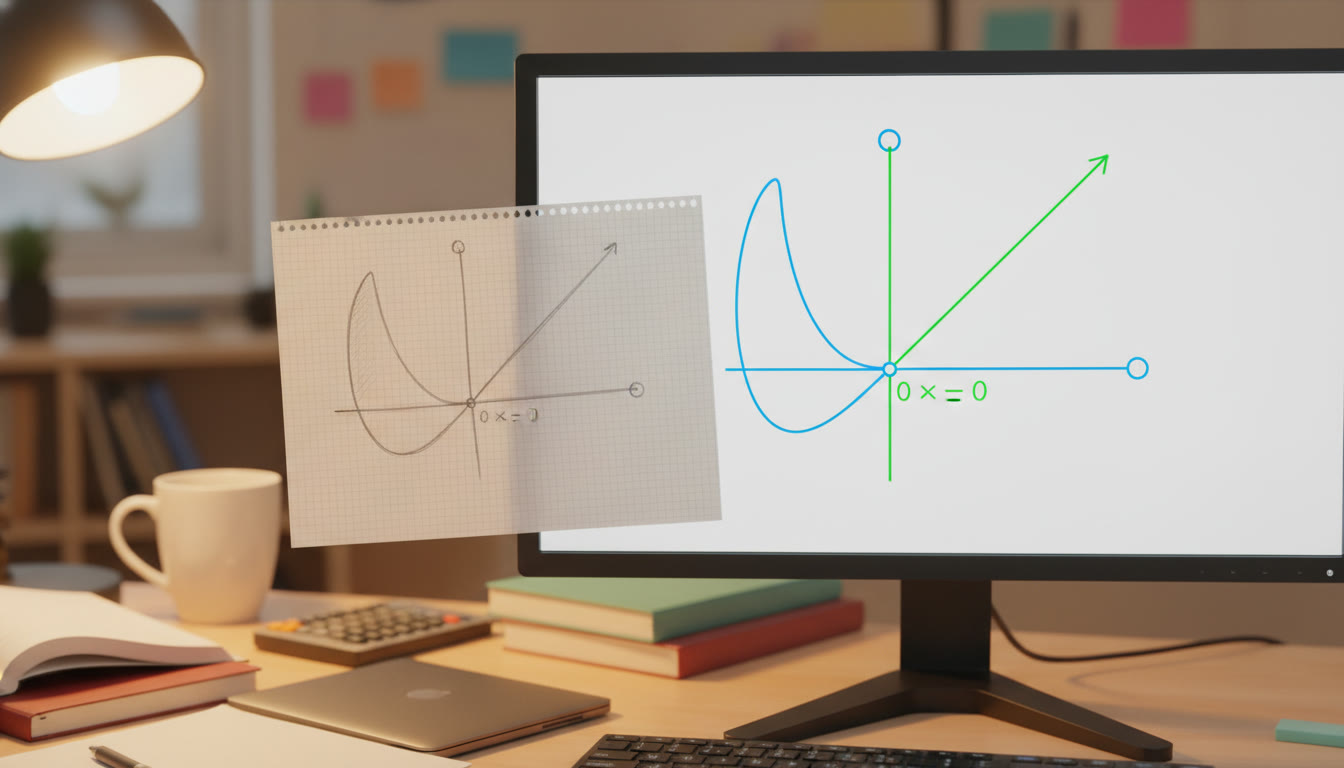
4. Transformations — Make a Graph Your Own
Understanding transformations lets you quickly sketch a complicated-looking graph by starting from a known basic curve and shifting, stretching, reflecting, or compressing it. Key moves to master:
- Vertical shifts: f(x) + k moves the graph up/down.
- Horizontal shifts: f(x − h) moves it right/left.
- Vertical stretch/compression: a·f(x) scales outputs.
- Horizontal stretch/compression: f(bx) scales inputs (watch the reciprocal effect).
- Reflections: −f(x) flips over the x-axis; f(−x) flips over the y-axis.
Modeling: How to Turn Data or a Story Into a Function
Step-by-Step Modeling Method
Modeling is a skill that mixes intuition with technique. Use this simple workflow:
- Read the problem carefully — identify variables and units.
- Decide which function family seems appropriate from context or data shape.
- Fit parameters using points or regression (when allowed/available).
- Check domain and interpret any restrictions in context.
- Validate: compare predictions with data or test limiting behavior.
- Refine if necessary — sometimes a piecewise model or a different family fits better.
Example: Modeling Savings With Exponential Growth
Imagine you deposit $1,000 in an account that grows at 4% annual interest compounded yearly. The exponential model is A(t) = 1000(1.04)^t, where t is years. Simple, interpretable, and powerful: it tells you doubling time roughly via the rule of 72 (72 ÷ 4 ≈ 18 years).
Example: Piecewise Model for Speed Limits
A commuter’s average speed in a city might be piecewise: a slower portion during rush hour and a faster portion at night. A piecewise function models each time interval with a different linear rule. This often captures behavior much better than trying to force a single smooth function to fit everything.
Graphing and Visual Intuition — Your Secret Weapon
Read the Shape Before You Compute
Before doing heavy algebra, glance at the graph or sketch the rough shape. Ask: Is it increasing or decreasing? Are there asymptotes? Where are the zeros? This habit saves time on tests and helps avoid algebraic mistakes because your intuition provides a quick check on whether answers are reasonable.
Important Graph Features to Spot Quickly
- Intercepts — where the graph crosses axes.
- Zeros — where f(x) = 0; useful for factorization checks.
- Asymptotes — vertical (where denominator = 0), horizontal (end-behavior), or slant.
- Local extrema and intervals of increase/decrease — tell the story of behavior.
- Continuity and smoothness — are there jumps, corners, or removable holes?
Practice Strategies and Study Plan (Built for AP Success)
A Weekly Study Rhythm
Consistency beats last-minute cramming. Here’s a recommended schedule you can adapt to a busy week:
| Day | Focus | Time |
|---|---|---|
| Monday | Concept review (definitions, domain/range, function types) | 45–60 min |
| Wednesday | Graph sketching and transformations practice | 45 min |
| Friday | Modeling problems and real-data fits | 60 min |
| Weekend | Mixed practice set and error review | 90–120 min |
Active Practice Beats Passive Reading
Do problems, then explain your reasoning out loud or in writing. When you get a question wrong, don’t just mark it — analyze: Was it a conceptual error, algebra slip, or misread of the question? Keep an error log and revisit those problem types until you consistently get them right.
Quality Over Quantity: Target Weak Spots
A focused 30-minute session on inverse functions or asymptotes will yield more improvement than an unfocused 2-hour block doing random problems. Use short, intense practice sessions targeting your weak areas.
Exam Techniques: How to Turn Knowledge Into Points
Multiple Choice Tips
- Predict before you look at choices — this avoids trap answers.
- Use answer elimination: often one or two choices are obviously wrong.
- Backsolving: plug answer choices into the original condition if algebra is messy.
Free-Response Tips
- Show your work clearly: partial credit is real — document algebra steps and reasoning.
- Label units and define variables when modeling (this earns easy points and clarifies thought).
- Before finalizing, quickly re-check numeric computations and units.
Common Pitfalls and How to Avoid Them
Pitfall: Confusing f(x) with Multiplication
Remember that f(x) denotes the output of a function evaluated at x. f(x + 1) is not f(x) + 1 unless the function is linear with unit slope. Always substitute carefully.
Pitfall: Domain Oversights
Don’t forget to exclude values that make denominators zero or that break the context of a real problem (like negative time). When in doubt, mention domain restrictions in your solution.
Pitfall: Misreading Transformations
Horizontal and vertical shifts often trip students: f(x − 2) moves right, not left. Draw a small sketch each time until the idea is second nature.
Worked Problem: From Story to Function (Step‑by‑Step)
Problem: A small town’s population starts at 10,000 and grows at 3% per year for the first 5 years, then slows to 1% per year afterward. Model the population and estimate it after 8 years.
Solution approach:
- Recognize a piecewise exponential model is appropriate because the growth rate changes after year 5.
- For 0 ≤ t ≤ 5, P(t) = 10000(1.03)^t.
- For t > 5, use continuity at t = 5: P(5) = 10000(1.03)^5. For t = 5 + s, P(t) = P(5)·(1.01)^s.
- To find P(8), set s = 3: P(8) = 10000(1.03)^5(1.01)^3. Compute numerically for a final answer.
Note how modeling choices (piecewise, continuity) reflect real-world reasoning rather than algebraic trickery alone.
How to Use Technology Wisely
Graphing calculators and software are tools — they should extend your intuition, not replace it. Use them to:
- Quickly visualize functions and test hypotheses about behavior.
- Perform regression to find best-fit parameters for modeling tasks (if allowed during practice).
- Check algebraic work and compute numerical approximations accurately.
But don’t skip hand-sketching: exams sometimes test your ability to reason without a device, and manual sketching builds deeper understanding.
Using Personalized Tutoring to Accelerate Progress
Targeted guidance can make a huge difference when you’re aiming for a top AP score. Sparkl’s personalized tutoring offers 1-on-1 guidance, tailored study plans, expert tutors, and AI-driven insights that help you focus on the concepts and problem types that matter most. When you’re stuck on inverse functions, asymptotes, or building a modeling approach from messy data, a focused session can both clarify the idea and show you efficient exam strategies.
Checklist Before You Move On to Unit 2
Before leaving Functions & Modeling, ensure you can confidently:
- Define a function and move between its representations.
- Sketch basic function families and apply transformations.
- Identify domain and range in context and algebraically.
- Fit simple models to data and explain why you chose that model.
- Interpret graphs and write matching algebraic expressions (and vice versa).
Quick Reference Table: Function Families and Key Features
| Function Type | Basic Form | Key Feature | Good For Modeling |
|---|---|---|---|
| Linear | f(x) = mx + b | Constant rate of change | Simple trends, budgets, velocity (constant) |
| Polynomial | f(x) = ax^n + … | Turns and smooth curves | Trajectories, fitting smooth data |
| Rational | f(x) = p(x)/q(x) | Vertical asymptotes, holes | Rates with singularities, chemical concentrations |
| Exponential | f(x) = a·b^x | Multiplicative growth/decay | Population, compound interest, radioactive decay |
| Logarithmic | f(x) = log_b(x) | Slow growth after rapid increase | Sound intensity scales, Richter scale-like measures |
| Trigonometric | f(x) = A sin(Bx + C) + D | Periodicity | Waves, seasonal patterns |
Final Tips — Habits of Top Scorers
- Explain your answers: writing a short sentence interpreting your final value turns an algebraic result into a complete, high-quality solution.
- Practice under timed, exam-like conditions to build speed and accuracy.
- Work with a tutor for targeted improvement — brief sessions focusing on your weakest subtopics often deliver the largest gains. Sparkl’s approach to tailored study plans and 1-on-1 tutoring is designed for this kind of efficient progress.
- Teach someone else a concept — if you can explain transformations, inverses, or modeling to a friend, you truly understand it.
Wrapping Up: Make Unit 1 Your Foundation
Functions and modeling are the foundation of AP Precalculus. Spend time understanding not just how to compute, but why methods work and when to choose one model over another. Build habits of sketching, questioning, and checking. Use technology to accelerate learning, and consider personalized help when you hit a persistent wall — a targeted bit of coaching can turn confusion into clarity quickly. With steady practice and the right strategies, you’ll move into Unit 2 with confidence and momentum.
Good luck — and remember: learning functions is learning to tell the story of change. Once you can tell that story clearly, the rest of Precalculus becomes much more enjoyable (and a lot less mysterious).



















No Comments
Leave a comment Cancel