Why These Edge Topics Matter — and Why You Can Master Them
If you’re taking AP Calculus BC, you’ve already climbed a mountain of function behavior, integrals, and differential equations. But there are two topics that often separate the good from the great: tight understanding of series error bounds and confident work with polar area integrals. They show up on the exam in neat little traps: a subtle remainder estimate here, a tricky conversion to polar there. With a few clear strategies and rapid-fire routines, you can turn these worries into reliable points.
What This Post Will Give You
- Crunchable explanations of series error bounds (remainder terms) and polar area computation.
- Fast-check strategies and mnemonic cues for exam day.
- Worked examples that you can replicate under time pressure.
- A sample study routine and a comparative table summarizing what to watch for.
- How targeted help—like Sparkl’s personalized tutoring—can give you 1-on-1 guidance and tailored study plans to cement these skills.

Part I — Series Error Bounds (Remainder Estimates) Fast-Track
At-a-glance: What is an error bound?
When you approximate a function by a partial sum of a series (think Taylor or Maclaurin polynomial), the error bound—often called the remainder—tells you how far off that approximation might be. On exams, you’re usually asked for one of three things: the remainder formula, a numeric bound for the remainder, or an assurance that the approximation is within a specified tolerance.
Core idea in one sentence
Use the appropriate remainder formula (Lagrange form for Taylor series or alternating series estimation when applicable), then bound the unknowns to produce a clean inequality that answers the question.
Which remainder formulas matter most?
- Lagrange Remainder (Taylor): R_n(x) = f^{(n+1)}(c) * (x – a)^{n+1} / (n+1)! for some c between a and x. You rarely know c, so you bound f^{(n+1)}(c) on the interval.
- Alternating Series Estimation Theorem (AS): If the alternating series meets the monotone decreasing and limit-to-zero conditions, then |R_n| ≤ next term in magnitude.
- Integral Test Remainder: For positive decreasing functions, the remainder can be bounded by integrals: ∫_{n+1}^∞ f(x) dx ≤ R_n ≤ ∫_{n}^∞ f(x) dx.
Rapid-fire checklist for tackling a remainder problem
- Identify the series type: Taylor/Maclaurin? Alternating? Positive-term series?
- Pick the right remainder tool: Lagrange, Alternating Series Estimation, or Integral Test.
- Locate the interval for c (if using Lagrange). Find a usable bound for the derivative.
- Simplify algebraically and compare to the asked tolerance (e.g., 0.001).
- If solving for n, isolate n and use inequalities, Stirling intuition, or trial check small n values.
Worked Example 1 — Lagrange remainder, straightforward
Problem: Using the Taylor polynomial centered at a = 0 (Maclaurin), approximate e^x at x = 1 with error less than 0.0005. How many terms do you need?
Step 1: Taylor series for e^x: Σ_{k=0}^∞ x^k / k! . The (n+1)-th derivative is also e^x, so on [0,1] the derivative is ≤ e.
Step 2: Lagrange remainder bound: |R_n(1)| ≤ e * 1^{n+1} / (n+1)! = e / (n+1)!. We want e / (n+1)! < 0.0005.
Step 3: Trial values: 6! = 720 gives e/6! ≈ 2.718/720 ≈ 0.00377 (too big). 7! = 5040 → ≈ 0.000539 (slightly above). 8! = 40320 → ≈ 6.7e-5 (works). So n+1 = 8 → n = 7. Use the 7th-degree polynomial.
Exam tip: Tabulate small factorials in your scratch for quick trials—this beats messy algebra under time pressure.
Worked Example 2 — Alternating Series Estimation
Problem: For the alternating series Σ (-1)^{n+1} / n^2, how many terms ensure the remainder is ≤ 0.001?
Step 1: Check conditions: terms 1/n^2 decrease monotonically to 0, so AS estimation applies. The magnitude of the remainder ≤ the next term: 1/(n+1)^2 ≤ 0.001.
Step 2: Solve: (n+1)^2 ≥ 1000 → n+1 ≥ √1000 ≈ 31.62 → n ≥ 30.62. So n = 31 terms are required.
Part II — Polar Areas Rapid-Fire
What’s different about polar area?
Polar area uses r and θ. When a region is defined by r(θ), the area between two angles θ = a and θ = b is found with the integral 1/2 ∫_a^b r(θ)^2 dθ. That squared radius factor is the key structural difference from Cartesian area. Converting bounds, recognizing loops, and handling negative r values are where most mistakes happen.
Quick rules you must keep front-of-mind
- Area formula: A = (1/2) ∫_{α}^{β} [r(θ)]^2 dθ.
- If the curve loops back (petals), identify proper θ-intervals for each piece; compute each petal’s area and add if needed.
- Watch the square! r could be negative for some θ; because of the square, area contribution is still positive, but the curve tracing direction matters when identifying bounds.
- For intersections between two polar curves r1(θ) and r2(θ), solve r1(θ) = r2(θ) for θ to find limits.
Rapid-fire checklist for a polar area problem
- Sketch (quick) the polar curve or at least mark symmetry/petals.
- Find intersections or natural θ limits (0 to 2π, 0 to π, or smaller intervals for petals).
- Apply A = 1/2 ∫ r^2 dθ. Simplify r^2 before integrating if possible.
- Break into symmetric pieces if helpful and multiply by symmetry factor.
Worked Example — Single petal area
Problem: Find area of one petal of r = cos(3θ).
Step 1: Recognize petals: For r = cos(3θ), over [0, 2π] there are 3 full petals because the frequency 3 creates three repeats. One petal occurs when cos(3θ) ≥ 0. For the first petal, take θ from -π/6 to π/6 (centered around 0).
Step 2: Area for one petal: A = (1/2) ∫_{-π/6}^{π/6} cos^2(3θ) dθ.
Step 3: Use identity cos^2(u) = (1 + cos 2u)/2. Then integrate easily. The algebra yields a tidy positive area; symmetry simplifies the evaluation because the cos(6θ) term integrates to zero over symmetric limits.
Common Pitfalls and How to Dodge Them
Series error bounds pitfalls
- Forgetting to bound derivatives on the correct interval for the Lagrange remainder. If you’re approximating around a = 0 but evaluating at x = 2, bound the derivative on [0,2] (or [-, +] accordingly).
- Using the alternating series estimate when terms aren’t monotone decreasing; check monotonicity first.
- Confusing the next term size with factorial growth—when solving for n, trial-and-error with small factorial table entries is faster than trying to solve factorial inequalities analytically.
Polar area pitfalls
- Using Cartesian-intuition: polar curves can retrace themselves—drawing rough traces avoids double-counting.
- Ignoring symmetry that could reduce integral work; many polar curves have rotational symmetry that makes life easier.
- Mis-handling negative r values—remember r^2 makes area positive but mapping to θ intervals can change.
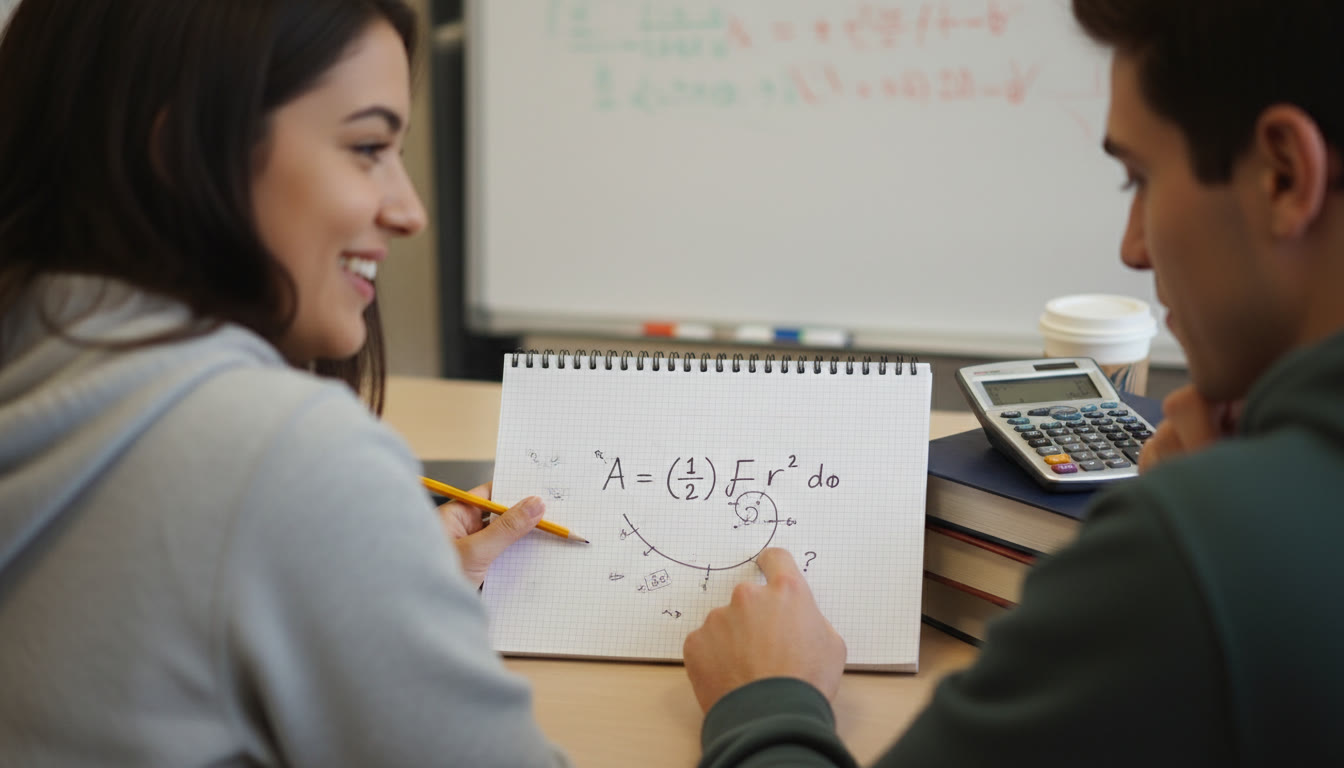
Strategies to Prepare Quickly (2–3 Week Sprint)
Whether you have two weeks or three before a big mock exam, here’s a compact plan to build speed and accuracy.
Week-by-week actionable plan
- Week 1 — Concept Lockdown: Spend three focused sessions on remainder theory: Lagrange form, alternating series test, and integral test. Do 6–8 problems per session including a mix of symbolic and numeric remainder problems.
- Week 2 — Polar Practice + Integration Skills: Block sessions for polar plotting, identifying petals, and computing areas. Combine with substitution practice and trigonometric identities to speed up integrating r^2.
- Week 3 — Mock Conditions: Timed 45–60 minute mixed sets including both series remainder and polar area problems. Use error analysis to correct one misconception each day.
Small habits that pay big dividends
- Keep a running mini-table of factorials up to 10! in your formula sheet for quick trials.
- When bounding derivatives, explicitly state the interval on your scratch paper—this both avoids mistakes and helps graders follow your logic.
- Create a small list of common trig identities you’ll need for r^2 integration (cos^2, sin^2, double-angle, product-to-sum).
Concise Comparison Table: Series vs. Polar Area Key Moves
| Aspect | Series Error Bounds | Polar Areas |
|---|---|---|
| Main Formula | Lagrange Remainder or Alternating Series Estimate | A = (1/2) ∫ r(θ)^2 dθ |
| Typical Mistake | Wrong interval for derivative bound | Wrong θ-limits or double counting petals |
| Fast Strategy | Use monotonicity or next-term bound when possible | Use symmetry and square identities to simplify |
| When to use trial n | When factorials are involved and inequality solving is messy | Not applicable |
| When AS applies | Alternating decreasing terms to 0 | Not applicable |
Sample Rapid-Fire Problem Set (do 10 under 25 minutes)
Use these to sharpen timing. Try to do each in ~2–3 minutes and check work within 30 seconds.
- Bound the remainder for sin(x) approximated by first three nonzero terms at x = 0.5 with tolerance 10^(-4).
- For Σ (-1)^{n} (x)^{n}/n!, determine the remainder bound after 4 terms at x = 2.
- Find area inside r = 2 sin θ from θ = 0 to θ = π.
- Compute area of one petal of r = sin(2θ).
- Given f^{(n+1)}(x) ≤ M on [0,1], write an expression for |R_n| with explicit M for e^x.
- Use the integral test to bound Σ_{k=n+1}^∞ 1/k^p for p > 1 with an integral expression.
- Show how to handle r = 1 + 2 cos θ for area enclosed where r ≥ 0 in [0, 2π].
- Solve how many terms needed for alternating series Σ (-1)^{n}/(n!) to have error < 10^-5.
- Sketch and compute intersection points of r = cos θ and r = 1/2 and find area between them.
- Explain in three lines how to pick θ-bounds for r = cos(3θ) petals.
How Personalized Tutoring Can Speed Your Progress (Short Note)
If you’re struggling to translate these strategies into fast exam answers, targeted help can cut weeks off your solo practice. Sparkl’s personalized tutoring offers 1-on-1 guidance, tailored study plans, expert tutors who know the AP Calculus BC exam, and AI-driven insights that identify your specific weaknesses (for example, whether you confuse Lagrange remainder intervals or mishandle polar bounds). A few focused sessions—one to fix conceptual gaps and a couple to run timed problem sets—often yields a sharp rise in accuracy and confidence.
Final Exam-Day Tips — Calm, Clear, and Confident
- Read the question twice. Identify whether it’s asking for a numerical bound, proof of convergence, or a definite integral area.
- Write the formula you plan to use immediately. Hypothesize the remainder type or polar interval so you don’t drift mid-solution.
- Use symmetry. If a curve’s petal repeats, integrate one and multiply — that saves time and reduces algebra errors.
- When solving for n, don’t overcomplicate: trial small values for factorial-based inequalities; use a calculator only to confirm final checks if allowed.
- Box your final answer and state any assumptions (e.g., “bounded derivative M ≤ e on [0,1]”) so graders see your reasoning even if arithmetic slips.
A Little Encouragement
Edge topics can feel intimidating because they demand a tidy mix of conceptual understanding and algebraic fluency. But they’re also highly teachable—one good explanation and a few well-chosen practice problems often unlock them. Make a habit of short, deliberate practice sessions focused on a single technique (e.g., “today: Lagrange remainder bounds” or “today: identifying θ-limits for petals”) and you’ll convert confusion into consistent points on the AP exam.
Parting Assignment
Tonight: pick two problems—one remainder bound and one polar area—from a practice set. Time yourself, then review mistakes and rewrite a one-paragraph solution that a classmate could follow. If you find a recurring mistake, that’s the exact moment to ask for 1-on-1 help (and that’s where Sparkl’s tailored tutoring can help turn a persistent error into a clear strategy).
Now take a deep breath. You’ve got the map—routines, quick checks, and a study plan. Edge topics aren’t unbeatable; they’re predictable. Play them with strategy, and they’ll reward you with points.
Good luck—and study smart.

















No Comments
Leave a comment Cancel