Welcome to Rotation: Why τ = r × F Actually Makes Sense
If you’ve ever pushed a door and watched it swing open, you’ve already seen torque in action. That simple everyday moment hides a compact mathematical idea: τ = r × F. In AP Physics 1, mastering this relationship isn’t about memorizing symbols — it’s about developing an intuition for how forces cause rotation. In this blog we’ll unpack the geometry and physics behind torque, practise with clear examples, compare torque to force, and give you study strategies that stick. Along the way, I’ll point out how one-on-one guidance — like Sparkl’s personalized tutoring, with tailored study plans and expert tutors — can accelerate the moment when these ideas finally click.
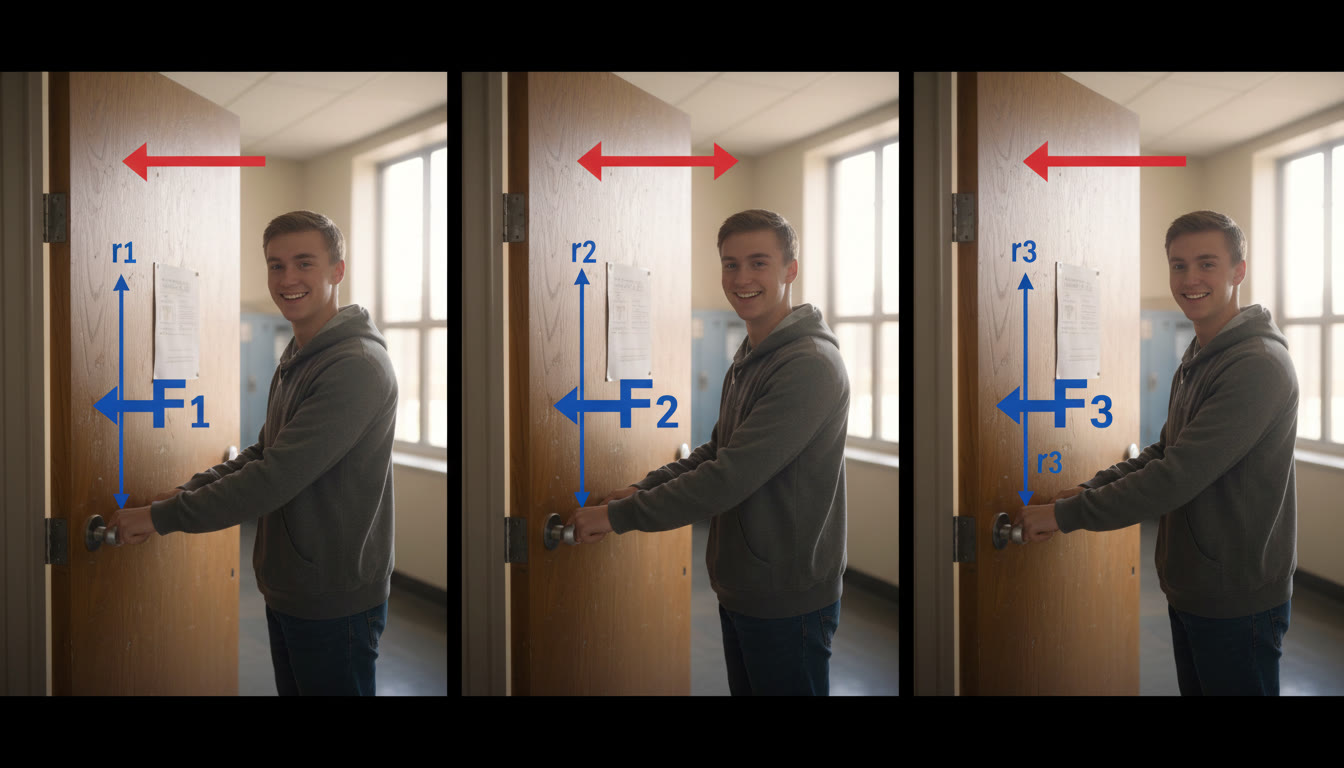
Start with a Picture: What Is Torque?
Torque is the rotational analogue of force. Where force tends to cause linear acceleration (F = ma), torque tends to cause rotational acceleration (τ = Iα). But torque is not just ‘how hard’ you push — it’s also where you push. Pushing a door near the hinge does almost nothing; push at the edge and the door swings easily. That difference is encoded in τ = r × F.
The Pieces of the Equation
- τ (tau): The torque vector. Its magnitude is how strong the twist is; its direction follows the right-hand rule.
- r: The position vector from the axis of rotation (think hinge) to the point where the force is applied.
- F: The force vector you apply.
- × (cross product): A vector operation whose magnitude equals r F sin(θ), where θ is the angle from r to F, and whose direction is perpendicular to the plane containing r and F (right-hand rule).
Intuition: Why the Cross Product?
At first glance, a cross product feels like abstract vector algebra. But each element has a physical meaning:
- r tells you how far from the axis you are applying the force — longer r gives more leverage.
- F tells you how strong the push is.
- sin(θ) picks out the component of the force that actually tries to rotate the object (the component perpendicular to r).
Imagine the force is perfectly radial — pointing directly toward or away from the hinge (θ = 0 or 180°). Then sin(θ) = 0, and τ = 0: pushing straight toward the hinge doesn’t make it rotate. Now imagine the force is tangential (θ = 90°). Then sin(θ) = 1, and you get the maximum torque for that r. The cross product succinctly packages these geometric facts into one clean expression.
Right-Hand Rule: Which Way Does the Object Want to Turn?
The direction of τ is given by the right-hand rule. Point your fingers along r, curl them toward F, and your thumb points in the direction of τ. For AP Physics 1 you’ll often use the sign of torque (positive/negative) in a chosen axis direction rather than worrying about the vector’s physical orientation in space — but understanding the rule helps with signs and three-dimensional thinking.
Working Through Concrete Examples
Examples move torque from abstract to tangible. We’ll step through three cases: a door, a wrench, and an off-center push on a merry-go-round.
1) The Door — Push at Different Distances
Take a door of width 0.9 m. You apply a 10 N force perpendicular to the door surface. Compute the torque when you push at 0.15 m from the hinge and at 0.9 m.
- At r = 0.15 m (near hinge): τ = rF = 0.15 × 10 = 1.5 N·m.
- At r = 0.90 m (edge): τ = 0.90 × 10 = 9.0 N·m.
Conclusion: Pushing near the hinge produces much less rotational effect. That’s leverage.
2) The Wrench — Angle Matters
Using the same 10 N force, suppose you push with the force at 60° to the wrench handle (not perpendicular). The magnitude of torque is τ = rF sin(θ). For r = 0.25 m and θ = 60°, τ = 0.25 × 10 × sin(60°) = 2.5 × 0.866 ≈ 2.16 N·m. Compare that to pushing perpendicular (θ = 90°) where τ = 2.5 N·m. The 60° push is less effective because some of the force is partly pulling or pushing along the handle instead of turning it.
3) Merry-Go-Round — Off-Center Push
Imagine standing on the rim of a circular platform and someone pushes you. If they push tangentially you start rotating easily; if they push radially, you slide inwards or outwards but don’t start rotating. This illustrates the sin(θ) factor again, and also shows that torque depends on where the force is applied relative to the center.
Table: Quick Reference for Common Torque Scenarios
| Scenario | r (m) | F (N) | θ (degrees) | Torque Magnitude (N·m) | Practical Tip |
|---|---|---|---|---|---|
| Door near hinge | 0.15 | 10 | 90 | 1.5 | Move farther from hinge to increase torque |
| Door at edge | 0.90 | 10 | 90 | 9.0 | Max torque for given force |
| Wrench, 60° push | 0.25 | 10 | 60 | ≈2.16 | Align force perpendicular for best effect |
| Radial push on disk | 0.50 | 15 | 0 | 0 | Radial force can’t cause rotation |
Torque vs. Force: A Helpful Comparison
It’s easy to confuse torque and force because both involve pushes and pulls. Here’s a compact way to think about it:
- Force (F): causes translation; think of accelerating the center of mass (F = ma).
- Torque (τ): causes rotation about an axis; think of accelerating angular velocity (τ = Iα).
- Both can act simultaneously. A single force may produce both a net force and a torque about a chosen pivot.
Example: A hammer hitting a nail imparts a force that pushes the nail straight (translation). If the hammer strikes off-center on a lever arm, it can also introduce torque and cause rotation. In AP problems you’ll often be asked to choose a pivot wisely: a pivot at a point where unknown forces act can simplify torque equations by eliminating unknown torques (their moment is zero if r = 0 for that force).
Solving Typical AP Physics 1 Problems with τ = r × F
AP-style questions often ask you to set net torque to zero (static equilibrium) or to relate torque to angular acceleration (dynamic problems). Let’s outline the typical approach.
Strategy for Static Equilibrium Problems
- Choose a convenient pivot point (often one that eliminates an unknown force).
- Write ∑τ = 0 about the pivot. Include signs (clockwise negative, counterclockwise positive, or vice versa consistently).
- Use τ = rF sin(θ) or compute perpendicular components: τ = rF⊥ = r⊥F.
- Solve for the unknown.
Strategy for Rotation with Angular Acceleration
Use ∑τ = Iα, where I is the moment of inertia about the rotation axis and α is the angular acceleration. Common moments of inertia (for AP level) include point mass m at distance r (I = mr^2), solid disk (I = 1/2 MR^2), and thin hoop (I = MR^2). Combine your torque expression with the appropriate I to find α or the required torque for a desired α.
Common Pitfalls and How to Avoid Them
- Mixing up r and r⊥: r is the full position vector; r⊥ is the perpendicular distance from the axis to the line of action of the force. If the force is not perpendicular, compute rF sin(θ) or find the perpendicular component first.
- Sign errors: Always pick a sign convention for clockwise and counterclockwise and stick to it throughout the problem.
- Forgetting the axis: Torque depends on the chosen axis. The same force will produce different torque values about different pivots.
- Using wrong moment of inertia: Check that your I matches the axis location and object shape (use parallel-axis theorem if necessary for off-center axes).
Tactics for the AP Exam: What to Practice
AP Physics 1 problems reward clear diagrams and neat organization. Here are targeted habits that make a difference:
- Always draw a diagram: label pivot, forces, distances, and angles.
- Write the torque equation in words first: “Sum of torques about hinge equals zero.”
- Keep units visible and consistent — torque is N·m, not J (energy) confusion.
- When given multiple forces, compute each torque separately and then sum algebraically using your sign convention.
- Practice converting between rF sin(θ), rF⊥, and τ = (perp distance) × F — they’re the same idea in different guises.
Worked Example: A Beam in Equilibrium
Consider a uniform beam of length L = 4.0 m and weight W = 200 N, hinged at its left end. A student applies a 150 N upward force at the right end. Find the hinge reaction force (vertical) and check rotational equilibrium.
Step 1: Choose the hinge as the pivot so hinge forces create no torque about the pivot (r = 0 for hinge forces). Step 2: Set ∑τ = 0. The beam’s weight acts at its center (r = L/2 = 2.0 m) producing a clockwise torque: τ_weight = 200 N × 2.0 m = 400 N·m (clockwise). The applied 150 N at the end produces counterclockwise torque: τ_student = 150 N × 4.0 m = 600 N·m (counterclockwise). Net torque: 600 − 400 = 200 N·m counterclockwise. That means the hinge must provide a reaction to produce an opposing torque — but because hinge vertical force passes through pivot, its torque is zero. Instead, equilibrium requires that the net torque be zero; therefore our assumption that only those two forces act is inconsistent. The missing piece is that the hinge provides a moment (or there is an additional support). In many textbook variants, there will be a support force elsewhere; carefully check the full problem statement. The key learning point for AP students: choosing the pivot simplifies the torque terms, but make sure you’ve accounted for all vertical forces when balancing linear equations (∑Fy = 0) in addition to ∑τ = 0.
How to Build Deep Intuition — Study Routines that Work
Turning these ideas into exam-ready skills takes the right practice routine:
- Active diagramming: Every practice problem begins with a clear sketch and labeled vectors.
- Variety of contexts: Mix doors, wrenches, beams, pulleys, and rotating discs to see torque in different forms.
- Explain out loud: Teach the steps to a friend (or to yourself). If you can explain why sin(θ) appears, you understand it.
- Timed practice: Work problems under time constraints to build speed without sacrificing clarity.
- Targeted help: Use short tutoring check-ins when you get stuck — personalized tutoring like Sparkl’s 1-on-1 guidance can zero in on misconceptions, produce tailored study plans, and offer practice problems that match the AP style.
Quick Reference Cheatsheet
- Torque magnitude: τ = rF sin(θ)
- Perpendicular form: τ = r⊥F
- Vector form: τ = r × F (direction by right-hand rule)
- Rotational equation: ∑τ = Iα
- Static equilibrium: ∑F = 0 and ∑τ = 0
Exam-Day Mindset: Confidence through Structure
On test day, follow a calm, consistent approach: read carefully, draw the diagram, define your pivot, write the torque terms before numbers, and check units. If you hit a tricky problem, pause and ask: can I choose a pivot that removes an unknown? Can I find a perpendicular distance instead of juggling angles? Those little structural moves save time and prevent algebraic messes.
Extra Practice Problem (Try This Yourself)
A 2.0 m long uniform rod of mass 3.0 kg is hinged at one end and held horizontally. A person applies an upward force at the free end to hold it in equilibrium. Find the force the person must apply. (Treat g = 9.8 m/s².)
Hints: Weight W = mg acts at center (r = 1.0 m). Choose hinge as pivot and set ∑τ = 0.
Work it out on paper; then compare with the approach: torque due to weight = (3.0 × 9.8) × 1.0 = 29.4 N·m; torque from upward force at end = F × 2.0 m, so F × 2.0 = 29.4 => F = 14.7 N.
When to Reach Out for Personalized Help
Rotation concepts often become easier when someone watches your diagrams and pinpoints exactly where the geometric or sign error creeps in. If you find repeating mistakes — consistently wrong signs, mixing up r and r⊥, or misapplying moments of inertia — a few targeted sessions with an expert tutor can turn weeks of frustrated practice into days of steady progress. Personalized tutoring like Sparkl’s can provide tailored study plans, one-on-one guidance, and AI-driven insights to track your growth and suggest the next topics to practice.
Final Takeaways — What to Remember
- Torque combines how hard you push and where you push (τ = r × F). Geometry matters.
- Use diagrams, choose pivots wisely, and keep a consistent sign convention.
- Translate between rF sin(θ), r⊥F, and the cross product depending on the problem.
- Practice varied contexts and explain your reasoning out loud to deepen understanding.
- Targeted tutoring and feedback can shorten the path from confusion to clarity; consider short sessions focused on torque setup and sign conventions if you’re stuck.
Parting Encouragement
Mastering τ = r × F is more than learning a formula — it’s building a way of seeing the world: where forces push, how distances magnify effort, and how geometry chooses what causes rotation. Keep the practice varied, stay curious about the physical meaning behind each step, and don’t hesitate to get help when a misconception persists. With clear diagrams, steady practice, and focused feedback, rotational motion will stop feeling mysterious and start feeling like one of your strongest tools in AP Physics 1.
Good luck, and enjoy the satisfying moment when an awkward torque problem becomes elegant and simple. You’ve got this.



















No Comments
Leave a comment Cancel